Fun with comparative advantage

A friend recommended Tyler Cowen and Alex Tabarrok's introductory economics textbook, Modern Principles of Economics, to me. It's been almost ten years since I took an economics class, so I decided to take a look. I think I have noticed an exception to the law of comparative advantage as it is presented by that book.  I figure that either I have made a mistake, or this exception is already very familiar to those in the know. If I'm right, the exception would have no real world significance whatsoever, but it might provide an interesting way of looking at why the law of comparative advantage is true. If I have made a mistake, hopefully someone will point that out in the comments.

Let's start with just laying out comparative advantage. Why is trade and the division of labor necessary? There are three basic reasons:

(1) Tastes differ. If wild blackberries grow on my land and wild strawberries grow on yours, and we each prefer the other kind of berries, we can make ourselves better off by trading.

(2) Specialization allows learning and economies of scale. The example given in the book is that, if each of us were forced to live in the wilderness, growing our own food, building our own shelter, and making our own tools and clothing, we would probably starve. But one modern farmer can grow food for thousands of people. This is because farmers can learn far more about farming than can people who also have to learn about tool making, weaving, building, etc. Specialization enables the development of more knowledge. Specialization also makes it possible to invest in useful equipment that would not be justified if you were only growing food for personal use. Tractors are more efficient than trowels or draft animals, but a subsistence farmer wouldn't be cultivating enough land for it to make sense to use a tractor.

(3) Comparative advantage.

[If you already know about comparative advantage, you can skip to the section "Fastistan vs. Slowistan" below; but maybe you will want to brush up like I did.]

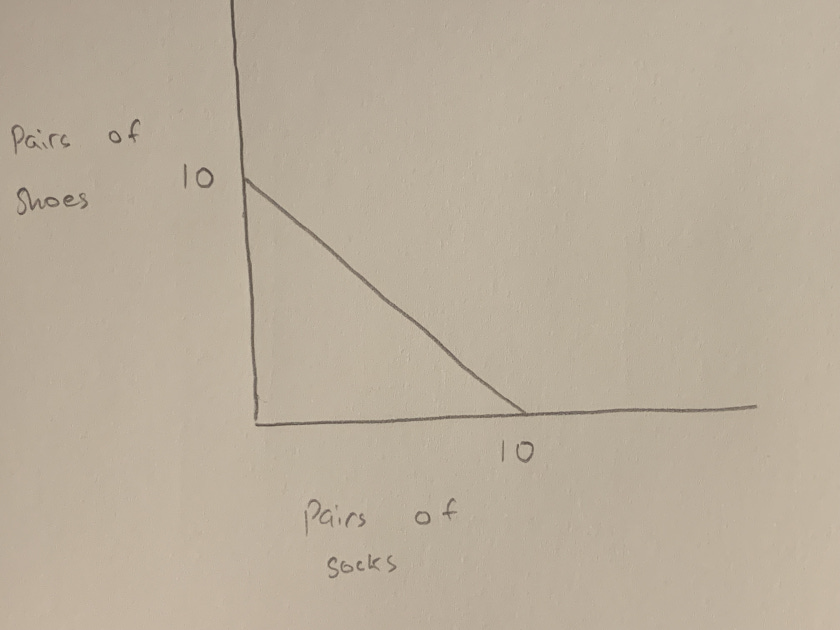
Imagine a world economy with two countries: Burkina Faso and Britain. This economy also has only two products: shoes and socks. Britain can produce 50 pairs of shoes per year, or 50 pairs of socks, or any combination of an equal number of pairs adding up to 50. This graph represents the possible combinations of shoes and socks that Britain can produce in a year:

Note that the slope of this "Production Possiblity Frontier" (PPF) is 1.

Burkina Faso can produce 10 pairs of shoes or 20 pairs of socks. Britain can produce more than Burkina Faso of both products--it has an absolute advantage.

Note that the slope of the PPF is 1/2.

What could Britain gain from a trading partner who, seemingly, brings nothing additional to the table?  

This is where comparative advantage comes in. Consider the opportunity costs of production for each country.

Because Britain can produce more of both products than Burkina Faso can, the cost in foregone production of producing in Britain is higher than in Burkina Faso. Therefore, both countries can be made better off by trade. As Cowen and Tabarrok put it: "The theory of comparative advantage not only explains trade patterns but it also tells us something remarkable: A country (or a person) will always be the low-cost seller of some good. The reason is clear: The greater the advantage a country has in producing A, the greater the cost to it of producing B" (pages 18-19).

Fastistan vs. Slowistan

Imagine two countries that are almost identical. The only difference is that in the first country, Fastistan, all productive machinery operates twice as fast as in the second country, Slowistan.

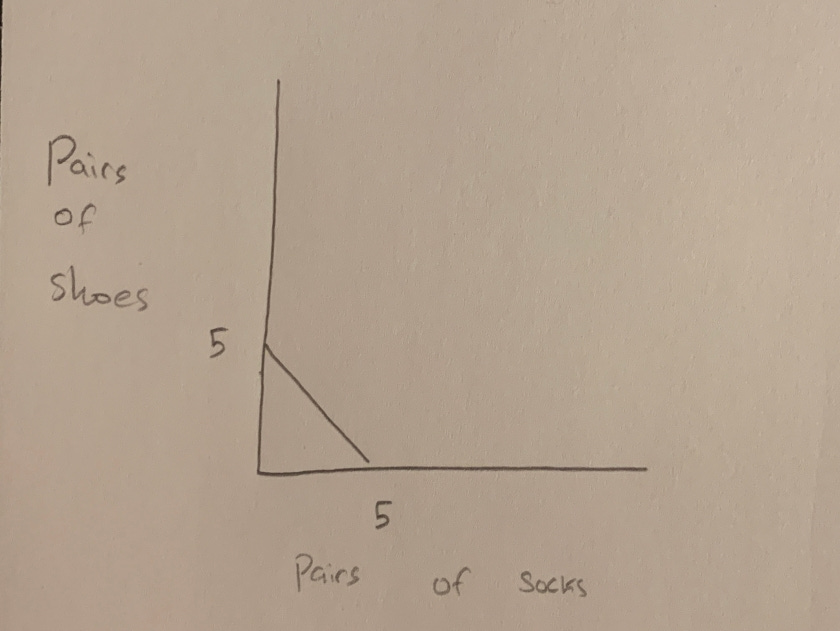
Fastistan can produce 10 pairs of shoes or 10 pairs of socks in a year.

Slowistan can produce 5 pairs of shoes or 5 pairs of socks.

Here are the opportunity costs of producing shoes and socks in Fastistan and Slowistan.

Note that the opportunity costs are the same. That is because, no matter how much more productive Fastistan is than Slowistan in absolute terms, what determines the unit opportunity cost is the per unit amount of foregone production. So if all products can be produced in the same ratio but in different amounts in two countries, the opportunity costs do not differ. It follows, I think, that neither country would be made better off by trade.

I don't think that this fact has any real world implications--you are unlikely to get a situation like that of Fastistan vs. Slowistan in the real world. Modern economies produce millions of different products. If there were really only two products, it might be possible in practice to get two countries with PPFs with the same slope. But such a thing is very, very unlikely with a PPF that exists in millions of dimensions.

That leads me to a few concluding questions:

1. If the PPFs have the same slope, there is no comparative advantage, only absolute advantage (I think). Does it follow that the more different the slopes of the PPF functions are, the greater the gains from trade?

2. How do economists model trade in real economies, which have more than a few products? I once was talking to an economist about some class of models, and I asked him if every product gets its own dimension, leaving you with an ultra-high dimensionality monstrosity. He said that in principle you could model it that way, but that actually was too complicated to do in practice. He then explained what they  do instead--but I don't recall what he said! How is this handled?